Total functional programming
Total functional programming (also known as strong functional programming[1], to be contrasted with ordinary, or weak functional programming) is a programming paradigm that restricts the range of programs to those that are provably terminating.
Termination is guaranteed through a restricted form of recursion, which operates only upon ‘reduced’ forms of its arguments. One such form is Walther recursion. In addition, every function must be a total (as opposed to partial) function. That is, it must have a definition for everything inside its domain. This may lead to unexpected or arbitrary definitions such as 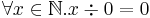
These restrictions mean that total functional programming is not Turing-complete. However, the set of algorithms that can be used is still huge. For example, any algorithm that has had an asymptotic upper bound calculated for it can be trivially transformed into a provably-terminating function by using the upper bound as an extra argument decremented on each iteration or recursion.
Another outcome of total functional programming is that both strict evaluation and lazy evaluation result in the same behaviour, in principle; however, one or the other may still be preferable (or even required) for performance reasons.
Total functional programming must necessarily also make a distinction between data and codata—the former is finitary, while the latter is potentially infinite. Such potentially infinite data structures are needed for applications such as I/O. Using codata entails the usage of such operations as corecursion.
Both Epigram and Charity could be considered total functional programming languages, even though they don't work in the way Turner specifies in his paper. So could programming directly in plain System F, in Martin-Löf type theory or the Calculus of Constructions.
Footnotes
- ^ This term is due to: Turner, D.A. (December 1995), Elementary Strong Functional Programming, "First International Symposium on Functional Programming Languages in Education", Springer LNCS 1022: 1–13.
References
- Turner, D.A. (2004-07-28), "Total Functional Programming", Journal of Universal Computer Science 10 (7): 751–768, doi:10.3217/jucs-010-07-0751, http://www.jucs.org/jucs_10_7/total_functional_programming